Равновеликие треугольники в трапеции доказательство. Трапеция. Свойства и элементы трапеции. Теоремы: признаки равнобедренной трапеции

Описанная окружность и трапеция. Здравствуйте! Для вас ещё одна публикация, в которой рассмотрим задачи с трапециями. Задания входят в состав экзамена по математике. Здесь они объединены в группу, дана не просто одна трапеция, а комбинация тел – трапеция и окружность. Большинство из таких задачек решаются устно. Но есть и такие на которые нужно обратить особое внимание, например, задача 27926.

Вписанные и описанные трапеции

Другими словами, учебники - это более быстрый момент для исправления: в стране насчитывается менее десятка крупных титулов, в отличие от тысяч учителей в стране. Мы должны убедиться, что эти глубокие концептуальные ошибки в учебниках сведены к минимуму, если не устранить.

Трапеция представляет собой четырехугольник, который имеет две параллельные стороны, а два других - нет, а сумма его углов равна 360º. На рисунке выше вы заметите, что две стороны параллельны, а две другие стороны могут рассматриваться как параллельные или расходящиеся.

Какую теорию необходимо помнить? Это:

Задачи с трапециями, которые имеются на блоге можно посмотреть здесь .

27924. Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.

Параллельные стороны называются основаниями трапеции, а расстояние между ними - это высота. Ответ: параллелограмм представляет собой многоугольник из четырех параллельных сторон два на два. Трапеция также представляет собой многоугольник из четырех сторон, но с 4 сторон, два - только параллельные.

Ответ: Да, потому что они имеют все 4 стороны и, кроме того, две-две параллели. Мы говорили, что трапеция имеет большую базу и небольшую, чтобы решить проблему, из которой они взяты? Базовое значение представляет собой среднее значение двух значений. В качестве основной базы ценность базы этой трапеции - полусумма обоих, то есть. Трапеция, которая имеет непараллельные стороны, равна равнобедренной трапеции.

Отметим, что описать окружность можно только около равнобедренной трапеции. Нам дана средняя линия, значит можем определить сумму оснований, то есть:

Значит сумма боковых сторон будет равна 22–10=12 (периметр минус основания). Так как боковые стороны равнобедренной трапеции равны, то одна сторона будет равна шести.

27925. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60 0 , большее основание равно 12. Найдите радиус описанной окружности этой трапеции.

Теоремы: свойства трапеции

Стороны и равны, следовательно, равнобедренная трапеция. Диагонали равнобедренной трапеции одинаковы. и те же. Это тот, который имеет два угла 90º. Как вы можете видеть, непараллельная сторона перпендикулярна и, следовательно, имеет два прямых угла. Диагонали разные и не перпендикулярны.

Ответ: Каждая трапеция представляет собой четырехугольник, но это не параллелограмм, потому что у него нет параллельных сторон от двух до двух. Он имеет только две параллели с четырех сторон. Прежде чем вы начнете их изучать, вы должны четко понимать концепцию симметрии.

Если вы решали задачи с окружностью и вписанным в неё шестиугольником, то сразу озвучите ответ – радиус равен 6. Почему?

Посмотрите: равнобедренная трапеция с углом при основании равным 60 0 и равными сторонами AD, DC и CB, представляет собой половину правильного шестиугольника:

Свойство диагоналей равнобедренной трапеции

Симметрия слова исходит из греческого син, означающего в то же время, и от слова метрона, означающего измерение. Мы нарисуем красную половину бабочки, которая у вас внизу. Две половины бабочки симметричны, то есть две половины имеют те же самые меры. Если эта бабочка с красной линией, которую мы называем осью симметрии, у вас она была в бумаге, а в двойнике - осью или красной линией, вы бы точно это увидели.

Если мы прорубим ось симметрии и удалим обе половины, мы увидим. Есть некоторые, которые говорят, что две половины одинаковы, другие идентичны. Истина заключается в том, что одинаковые и идентичные становятся одинаковыми, но эти две половины должны сказать, что они симметричны относительно оси, то есть оси симметрии.

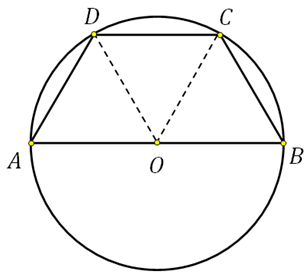
В таком шестиугольнике отрезок соединяющий противоположные вершины проходит через центр окружности. *Центр шестиугольника и центр окружности совпадают, подробнее

То есть большее основание этой трапеции совпадает с диаметром описанной окружности. Таким образом радиус равен шести.

Мы не говорим, что эти две половины бабочки одинаковы, хотя, хотя размеры и формы равны, однако их положение на плоскости не одно и то же, это наоборот. Чтобы узнать, совпадают ли два куска картона, вы ставите один поверх другого, и если они совпадают во всех своих точках, мы скажем, что они одинаковы. Если каждая из двух половинок бабочки помещает один поверх другого, правда в том, что они совсем не совпадают.

Диагональ равнобедренной трапеции

Давайте посмотрим на следующий рисунок, который очень легко рисовать, просто линейка и ручка. Это примерно половина простого обелиска. Чтобы закончить, нам нужна другая половина, нам не хватает ее симметричности, а именно. Если обе стороны расположены друг напротив друга.

*Конечно, можно рассмотреть равенство треугольников ADO, DOС и OCB. Доказать что они равносторонние. Далее сделать вывод о том, что угол AOB равен 180 0 и точка О равноудалена от вершин A, D, C и B, а и значит АО=ОВ=12/2=6.

27926. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.

Мы приближаемся к ним, и по точкам объединения двух половин мы рисуем красную линию, которую мы оставили. Если этот рисунок был на листе бумаги, вы увидите, что при складывании листа по красной линии или оси симметрии линии с одной стороны соответствуют тем, что расположены на другой стороне.

Геометрический элемент имеет только положение, не имеет размеров, длины, ширины или толщины. Точка может быть графически представлена падением. Помните, что представления представляют точку, но дело не в этом, так как точка на карте может представлять город, но это не город. Точки обычно обозначаются или идентифицируются столичной латинской буквой на стороне.

Отметим, что центр описанной окружности лежит на оси симметрии, при чём если построить высоту трапеции проходящую через этот центр, то она при пересечении с основаниями разделит их пополам. Покажем это на эскизе, также соединим центр с вершинами:

Положение линий в пространстве определяет их ориентацию: горизонтальную, вертикальную или наклонную. Параллельные линии - это прямые линии, которые, как бы долго они ни были, никогда не встречались, сохраняли одинаковое расстояние и никогда не пересекались. представляют собой две или более эквидистантные линии по всей длине.

Угол - это встреча двух прямых сегментов, ориентированных от общей точки. Пересечение между двумя сегментами называется вершиной угла, а стороны угла - двумя отрезками. Два угла являются последовательными, если одна сторона одного из них совпадает с одной стороной другого угла.

Отрезок EF является высотой трапеции, его нам нужно найти.

В прямоугольном треугольнике OFC нам известна гипотенуза (это радиус окружности), FC=3 (так как DF=FC). По теореме Пифагора можем вычислить OF:

В прямоугольном треугольнике OEB нам известна гипотенуза (это радиус окружности), EB=4 (так как AE=EB). По теореме Пифагора можем вычислить OE:

Два соседних угла смежны, если у них нет общих внутренних точек. Эти линии определяют четыре угла. Углы, которые не смежны, противоположны вершине. Мы говорим, что два угла конгруэнтны, если они накладываются друг на друга, все их элементы совпадают. Два противоположных угла вершины всегда конгруэнтны.

Конгруэнтные углы имеют равные измерения и наоборот углы, которые имеют равные измерения, являются конгруэнтными. Из двух указанных углов мы можем получить третий угол, измерение которого соответствует сумме измерений заданных углов. Единицей измерения угла в Международной системе является радиан.

Таким образом EF=FO+OE=4+3=7.

Теперь важный нюанс!

В этой задаче на рисунке чётко показано, что основания лежат по разные стороны от центра окружности, поэтому задача решается именно так.

А если бы в условии не было дано эскиза?

Тогда у задачи было бы два ответа. Почему? Посмотрите внимательно – в любую окружность можно вписать две трапеции с заданными основаниями.

Диагонали и стороны трапеции

Угол в 360 градусов - это угол, который завершает круг. После этого полного оборота этот угол совпадает с углом нуля градусов, но имеет величину 360 градусов. Чтобы получить приблизительную меру угла, нанесенного на бумагу, мы используем инструмент, называемый транспортиром, который содержит отрезок прямой в его основании, представляет собой полукруг сверху, обозначенный единицами от 0 до.

Заметные элементы и стороны многоугольника, углы, вершины и диагонали. Регулярный многоугольник имеет равные стороны и углы. Четырехугольник многоугольник имеет четыре стороны, четыре вершины, четыре угла и две диагонали. Они четырехугольники: параллелограммы, трапеции и трапеция - четырехугольник, который имеет две параллельные стороны, которые являются основой трапеции.

Раздел 2. Четырехугольники

I . Справочные материалы.

1. Трапеция, ее виды и свойства

Свойства трапеции, которые часто используются при решении задач:

1) Диагонали трапеции разбивают её на четыре треугольника с общей вершиной. Площади треугольников, прилежащие к боковым сторонам, равны.

2) В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения прямых, на которой лежат боковые стороны, лежат на одной прямой (точки М, N, О и К).

Параллелограмм представляет собой четырехугольник, противоположные стороны которого параллельны и конгруэнтны, а противоположные углы также конгруэнтны. Это параллелограммы: квадрат, прямоугольник, ромб и собственно параллелограмм. Трапеция: четырехугольник, который имеет две параллельные стороны, которые являются основой трапеции.

Теорема: свойство произвольной трапеции

Пентагон: многоугольник с пятью вершинами, пятью сторонами и пятью углами. Треугольник и многоугольник трех сторон, три угла и три вершины. Геометрический треугольник рисования равносторонний. Равносторонний треугольник - имеет три конгруэнтные стороны.

3) В равнобокой трапеции углы при основании равны.

4) В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии этой трапеции,

Мы называем треугольник объединением отрезков, образованных ими. точек. Внешний угол - это сумма несмежных интерьеров. Равнобедренные: две стороны с равными мерами. Скалайн: не имеет сторон с равными мерами. В каждом треугольнике большая сторона выступает против большего угла.

Если угол вершины А равен 80 °, мера θ обозначенного угла равна. Большой угол треугольника. у нас есть: Периметр:! Архитектор. 4√2 км 3 км. Полученный сегмент параллелен третьей стороне и измеряется его половиной. то. Теорема Объединяя середины двух сторон любого треугольника.

5) В равнобокой трапеции диагонали равны.

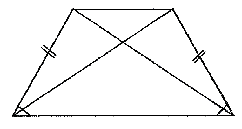
6) В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой их полусумме.

Каждый выпуклый четырехугольник, имеющий противоположные конгруэнтные углы, является параллелограммом. Диагонали конгруэнтны и разрезаны пополам и конгруэнтны. Диагональ алмаза не является конгруэнтным. Диагонали находятся под углами внутренних углов. находятся в биссектрисах внутренних углов.

Средняя Линия Треугольника

Рассматривая множества параллелограммов. Каждый квадрат - как ромб, так и прямоугольник. Можно сказать, что: три прямоугольника имеют одинаковую площадь. Соотношение между количеством мужчин и женщин в промышленном подразделении составляет 7 для показанного рисунка. Будем изучать выпуклые многоугольники.

7) Во всякой трапеции серединам боковых сторон и середины диагоналей лежат на одной прямой.

8) Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований.

Многоугольники получают различные наименования. Круг - это объединение окружности с ее внутренностью. Вычислите радиус этого круга. от высоты относительно наименьшей стороны € √. Фернандо. В 650 метрах от точки, где находится Фернандо. по прямой. в 350 метрах от отеля. Есть только один момент, когда вы можете одновременно слышать как Фернандо, так и Бруно. Жоао Гильерме и Бруно проиграли.

Фернандо достаточно кричит, что его можно услышать где угодно до 250 метров от того места, где он находится. также по прямой. Расстояние. Площадь треугольника равна 8 см². Таким образом. Ниже мы приводим краткое резюме и несколько упражнений с использованием теоремы Пифагора.

9) во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований.

10) Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.

11) Трапецию можно описать около окружности тогда и только тогда, когда сумма оснований равна сумме боковых сторон.

Наша цель в этой статье - показать применимость теоремы, ее важность в конструкциях посредством нескольких упражнений, которые решаются шаг за шагом. Отметим также, что из-за его важности теорема сильно заряжена в различных конкурсах. Итак, наслаждайтесь этой статьей, чтобы попрактиковаться и принять ваши сомнения.

Свойства средней линии трапеции

Теорема Пифагора; - Приложения; - Упражнения решены и многое другое. Утверждение теоремы Пифагора. В каждом прямоугольнике треугольника квадрат меры гипотенузы равен сумме квадратов мер ног. Бедра - это стороны правого угла, так как гипотенуза - это сегмент «спереди» под прямым углом.

2.Вписанные и o писанные четырёхугольники.

1)Если четырёхугольник вписан в окружность, то сумма противолежащих углов равна 180°.

Верно и обратное: если сумма противолежащих углов четырёхугольника равна 180°, то около этого четырёхугольника можно описать окружность.

2)Около параллелограмма можно описать окружность тогда и только тогда, когда этот параллелограмм есть прямоугольник.

Это было краткое резюме по теореме Пифагора, существует гораздо больше теории на эту тему. Но теперь давайте применим то, что было представлено выше в вопросах конкуренции, этого достаточно для нашей цели. Заявления ниже, а затем резолюции. Мильор Фернандес, в прекрасном уважении к математике, написал стихотворение, из которого мы извлекаем фрагмент ниже.

На многие листы книги математики. Инкогнитой. Он посмотрел на нее своим бесчисленным взглядом и увидел ее от вершины до основания: странная фигура. ромбовидные глаза, трапециевидный рот, прямоугольное тело, синусы сфероида. Он сделал свою жизнь параллельной ей, пока они не встретились в Бесконечном. «Кто ты?» - спросил он с сильным рвением. Я - сумма квадратов хиксов. Инкогнита ошибалась, чтобы сказать, кто она. Чтобы соответствовать теореме Пифагора, она должна дать следующее. ответ.

3)Около трапеции можно описать окружность, если она равнобокая.

четырёхугольник называется описанным около окружности, если окружность касается всех его сторон.

4)Если четырёхугольник описан около окружности, то суммы противолежащих сторон равны.

5)Если в выпуклом четырёхугольнике суммы противоположных сторон равны, то в этот четырёхугольник можно вписать окружность.

3. Площади четырёхугольников.

Площадь выпуклого четырёхугольника равна половине произведения диагоналей на синус угла между ними.

Ромб

1. Диагонали ромба взаимно перпендикулярны и делят углы пополам.

2. Площадь определяется формулами:

Параллелограмм

1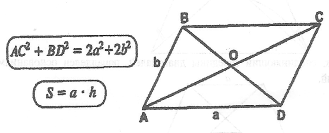. Сумма квадратов диагоналей равна сумме квадратов всех его сторон.

2. Площадь определяется формулой

II . Дополнительные материалы

1)Свойства вписанного выпуклого четырехугольника .

а)В выпуклом вписанном четырехугольнике сумма противоположных углов равна двум прямым

б)Обратно: если в выпуклом четырехугольнике сумма противоположных углов равна двум прямым, то около него можно описать окружность

Доказательство.

а) Пусть АВСD есть вписанный выпуклый четырехугольник; требуется доказать„ что

Так как сумма всех четырех углов сякого выпуклого четырехугольника равна 4d, то достаточно доказать только одно из требуемых равенств.

докажем, например, что

Углы В и D как вписанные, измеряются: первый-половиной дуги ADC, второй- половиной дуги АВС;

Следовательно, сумма

б) Пусть АВСD есть такой выпуклый четырехугольник, у которого

Через какие-нибудь три его вершины, например, через A,В и С, проведем окружность (что всегда можно сделать).

Четвертая вершина D должна находиться на этой окружности, пoтoму что в противном случае вершина угла В лежала бы или внутри круга, или вне его, и тогда этот угол не измерялся бы половиной дуги АВС; поэтому cyммa измерялась бы полусуммой дуг ADC и АВС и, значит, сумма Следствия

1) из всех параллелограммов только вокруг прямоугольника можно описать окружность.

2) около трапеции можно описать окружность только тогда, когда она равнобокая.

2) Свойство описанного четырехугольника. В описанном четырехугольнике суммы противоположных сторон равны.

Пусть АВСD будет описанный четырехугольник, Т.е, стороны его касаются окружности; требуется доказать, что АВ+СВ=ВС+АD

Обозначим точки касания буквами M, N, Р и Q. Так как две касательные, проведенные из одной точки окружности, равны, то АМ.=АQ, ВМ=ВN, CN=СР, DP=DQ.

Следовательно, АМ+МВ+СР+РD=AQ+QD+BN+NC. Т.е. АВ+СD=АD+ВС.

III . Вводные задачи.

Задача 1.

Средняя линия трапеции ABCD равна 15. AD – большее основание трапеции, A = 90°, D = 60°, BAC = 30°. Найдите длину стороны CD .

В ∆ABC (он прямоугольный) BC = – по свойству катета, лежащего против угла в 30°.

BAC = 30°, значит, CAD = 90° – 30° =
= 60°, следовательно, ∆ACD равносторонний,
т. е. AC = CD = AD = 2BC .

Средняя линия MN = 3BC = 30,

BC = 10, значит, CD = 2 · 10 = 20.

Ответ: 20.

Задача 2 .

Сторона AB параллелограмма ABCD равна а его диагонали равны 20 и 24. Найдите сторону BC .

Для любого выпуклого четырехугольника справедливо

где a , b , c и d – стороны четырехугольника, а d 1 , d 2 – его диагонали.

В параллелограмме

20 2 + 24 2 = 2(() 2 + b 2), b > 0; b 2 + 88 = 488,b 2 = 400, b = 20.

Задача 3 .

Основания трапеции равны 4 и 10, а ее боковые стороны – и 15. Найдите косинус наименьшего угла этой трапеции.

1) Проведем BM ∥ CD , значит, BMA =D , ВСDМ – параллелограмм, так как ВМ || MD , ВМ || СD . Следовательно, ВС = MD = 4,
BM = CD = 15, AM = AD – MD = 10 – 4 = 6.

2) В ∆AMB против большей стороны (выбирая из AB и BM ) лежит больший угол: AB BM, значит, BMA A .

Ответ: 0,8.

Задача 4.

Определите периметр равнобокой трапеции, у которой длина меньшего основания равна 7, диагонали перпендикулярны боковым сторонам и равны .

1) Проведем в трапеции ABCD высоту CF ,
тогда

∆ACD ∼ ∆AFC ,

2) Пусть FD = x , тогда AF = 7 + x

() 2 = (x + 7) (7 + 2x ),

36 · 2 = 49 + 21x + 2x 2 ,

2x 2 + 21x – 23 = 0,

D = 21 2 + 4 · 2 · 23 = 625,

х 1,2 =

3) Итак, AD = 7 +2 = 9;

P = 9 + 7 + 2 · 3 = 22.

Ответ: 22.

Задача 5.

В ромбе высота, проведенная из вершины тупого угла, делит сторону ромба пополам. Найдите периметр и высоту ромба, если меньшая диагональ его равна 7

1) В треугольнике ABD BK – высота и медиана, значит, ∆ABD -равнобедренный с основанием AD , т. е. AB = BD = 7 см. Тогда ∆ABD -равносторонний, значит, A = ABD = BDA = 60°.

2) P = 4AB = 4 · 7 = 28 (см).

3) BKD – прямоугольный, BK = AD sin BDK .

BK = 7 · sin 60° = (см). Ответ: 28 см; 3,5 см.

Задача 6.

Основание AB трапеции ABCD вдвое длиннее основания CD и вдвое длиннее боковой стороны AD . Длина диагонали AC равна 12, длина боковой стороны BC равна 5. Найдите площадь трапеции.

1) По условию AB = 2AD = 2DC .

Пусть M – середина AB , тогда AM = MB = CM ,
т. е. CM – медиана треугольника ABC и CM = AB , значит, ∆ABC прямоугольный с гипотенузой AB .Вершина C параллелограмма ABCD соединена с точкой N на стороне AB. Отрезок CN пересекает диагональ BD в точке P. Площадь треугольника BNP равна 8, а площадь треугольника BCP равна 12. Найдите площадь параллелограмма ABCD.

1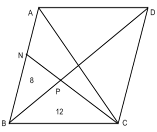) Треугольники BNP и BPC имеют общую высоту BH=>

SBNP/SBPC=PN/PC=>PN/NC=2/3;

2) Треугольники BPN и DPC подобны по

двум углам => SBPN/SDPC=(PN/PC) 2

SDPC=9/4; SBPN = (9/4)·8=18;

3) SBCD=SBPC+SDPC=12+18=30;

4) SABCD=2·SBCD=60; Ответ: 60

На стороне AB параллелограмма ABCD, как на диаметре, построена окружность, проходящая через точку пересечения диагоналей и середину стороны AD. Найдите углы параллелограмма.

Р

ешение:

1) По условию, AB – диагональ=> ABCD – ромб

P – середина АВ: по условию Q – середина AD=>PQ – средняя линия ∆ABD=BD=2PQ;PQ=R=>BD=2R;

PO=R – средняя линия ∆АBD=>AD=2·PO=R

∆ABD – правильный =>

Ответ: 60 o и 120 o .

Угол между сторонами АВ и СD четырехугольника ABCD=φ. Докажите, что AD 2 =AB 2 +BC 2 +CD 2 -2(AB·BCcosB + BC·CDcosC+CD·ABcosφ)

П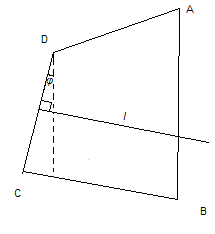о теореме косинусов AD 2 =AC 2 +CD 2 -2AC·CD·cosACD и AC 2 =AB 2 +BC 2 -2AB·BCcosB. A так как длина проекции отрезка АС на прямую l , перпендикулярную CD, равна сумме длин проекций отрезков АВ и ВС на прямую l, то ACcosACD=ABcosφ+BCcosC

V .Задачи для самостоятельного решения

№1. Докажите, что если ABCD прямоугольник, а Р- произвольная точка, то

АР 2 +СР 2 =DP 2 +BP 2

№2. Перпендикуляр, опущенный из вершины параллелограмма на диагональ, делит ее на отрезки длиной 6 и 15. Найдите большую сторону параллелограмма, если известно, что разность сторон равна 7.

№3. Одно из оснований трапеции равно 24, а расстояние между серединами диагоналей 4. найдите другое основание.

№4. Длины оснований равнобедренной трапеции относятся как 5:12, а длина ее высоты равна 17. Найдите радиус окружности, описанной около трапеции, если средняя линия равна высоте.

№5. В трапеции ABCD диагональ АС перпендикулярна боковой стороне СD. Окружность, описанная возле треугольника АВС, касается прямой CD, пересекает основание AD в точке М. Найдите площадь трапеции АBCD, если АМ=8, СМ=4.

№6. Окружность, центр которой лежит внутри квадрата PQRS, касается стороны PQ в точке К, пересекает сторону PS в точках А и В, а диагональ PR в точках С и D. Найдите радиус окружности, если АВ=16, СD=2√92

№7. В параллелограмме ABCD угол АВС=3п/4. окружность, описанная возле треугольника АВD, касается прямой CD. Найдите площадь параллелограмма, если диагональ BD=2

№8. Вершина С параллелограмма ABCD соединена с точкой N на стороне АВ. Отрезок CN пересекает диагональ BD в точке Р. Площадь треугольника BNP равна 8, а S ВСР =12. Найдите площадь параллелограмма АВСD.

№9. Найдите площадь трапеции, основания которой 6 и 26, а боковые стороны – 12 и 16.

Ответ: 153,6

№10. На стороне АВ параллелограмма АВСD как на диаметре построена окружность, проходящая через точку пересечения диагоналей и середину стороны АD. Найдите углы параллелограмма.

Ответ: 60,120,60,120.

VI . Контрольные задачи.

Вариант № 1.

1) В равнобедренную трапецию, площадь которой равна 80, вписана окружность радиуса 4. Найдите периметр трапеции.

2) Найдите диаметр окружности, вписанной в равнобедренную трапецию, если сумма оснований трапеции 26, а разность оснований равна 10.

3)В параллелограмме АВСД биссектриса угла С пересекает сторону АД в точке М и прямую АВ в точке К. Найдите периметр параллелограмма, если АК = 12, СМ = 24, МК = 18.

Вариант № 2.

1) В круг с площадью 169π вписана равнобедренная трапеция, меньшее основание которой равно 10. найдите площадь трапеции, если центр описанного круга лежит на её большем основании.

2) Найдите диаметр окружности, вписанной в равнобедренную трапецию, если сумма оснований трапеции 15, а разность оснований равна 9.

3)В параллелограмме АВСД биссектриса угла Д пересекает сторону АВ в точке К и прямую ВС в точке Р. Найдите периметр ∆ СДР, если ДК = 18, РК = 24, АД=15.

Вариант № 3.

1) В равнобедренную трапецию, площадь которой 20, а синус одного из углов равен 0,8, вписана окружность. Найдите радиус этой окружности.

2) Основание СМ и ОР трапеции СМОР равны 3 и 6 соответственно, диагонали трапеции пересекаются в точке Н, а площадь треугольника СРН равна 4. Найдите площадь трапеции.

3)В параллелограмме АВСД биссектриса угла С пересекает сторону АД в точке М и прямую АВ в точке К. Найдите периметр ∆ АМК, если СД = 12, СМ = 14, СВ = 30.

Вариант № 4.

1) Найдите площадь равнобедренной трапеции, если её высота равна 4, а тангенс угла между диагональю и основанием равен .

2) В равнобедренную трапецию, площадь которой равна 80, вписана окружность радиуса 4. Найдите периметр трапеции.

решении задач ...

Пояснительная записка 3 стр. Общие положения 3 стр. Общая характеристика учебного предмета. 3 стр. Цели и задачи изучения геометрии в основной школе 4 стр

Пояснительная записка

8 44 Решение задач по теме «Трапеция ». Комбинированный урок Закрепление знаний о свойствах и признаках параллелограмма и трапеции при решении задач . Знать...

Многоугольник, выпуклый многоугольник, четырехугольник. Параллелограмм, его свойства и признаки. Трапеция. Прямоугольник, ромб, квадрат, их свойства. Осевая и

Реферат

Обоснование которой не... трапеции , виды трапеций , формулировки свойств и признаков параллелограмма и равнобедренной трапеции , уметь их доказывать и применять при решении задач ... площади прямоугольника и использовать ее при решении задач типа 447 – ...

«Использование тригонометрии при решении планиметрических задач»